Have you ever considered the possibility of viewing your body as a donut? This whimsical analogy serves as a gateway to exploring the complexities of human anatomy and physiology in a delightful and engaging manner. By positioning ourselves alongside this beloved pastry, particularly in terms of dimensionality and internal functions, we can uncover profound insights into the essence of human operation, interaction, and existence. Join me on this enlightening journey, as we peel back the layers of this fascinating donut analogy!
The Challenge of a Two-Dimensional Perspective
To begin our exploration, let’s envision a two-dimensional (2D) existence, similar to drawing on a flat surface. In this simplified realm, life is devoid of depth and is limited to height and width. Picture stick figures as representations of people moving across a flat plane, where gravity still exerts its force downward toward the center of our "planet."
As one of these stick figures traverses the 2D landscape, it may encounter obstacles like a pole or wall. Unlike our rich three-dimensional world, where we can navigate around obstacles, in a 2D environment, the only options are to leap over or slide beneath barriers. Without the advantage of wings something we often take for granted in our three-dimensional reality our stick figure would face the arduous challenge of climbing over every single hindrance, much like Mario does in the classic video game "Super Mario Brothers.
"Thinking further about our human anatomy within such a two-dimensional framework reveals intriguing implications for our digestive systems. If our bodies were merely flat shapes, our digestive tracts would become incoherent and ineffective, splitting apart without the vital dimension of depth. This disconnection implies that complex multicellular organisms like ourselves, which rely on intricate systems of tubes and pathways, would be fundamentally incompatible with a 2D existence. Only simple single-celled organisms, indifferent to complex biological structures, might survive in such a world.
In this hypothetical 2D environment, every shape exists only in height and width. Upon slicing through a drawing of a human, the separation of top from bottom underscores a critical limitation of 2D representations: they fail to capture our continuous, three-dimensional reality. Conversely, our actual three-dimensional world boasts depth, enabling us to visualize, manipulate, and interact with objects meaningfully and coherently. This complexity illuminates how our analogy of the donut gains clarity and depth.
Transitioning to the Three-Dimensional World
The shift from a flat representation to our fully realized three-dimensional reality showcases the vast intricacies of human anatomy that would be lost in two dimensions. Humans exist with height, width, and depth, creating a rich tapestry of interconnected systems that sustain life and functionality.
Humans as "Donuts": An Internal Structure
Our digestive system is a remarkable tube that begins in the mouth and concludes at the anus, spanning a delightful 12 to 15 feet (or roughly 3.5 to 4.5 meters). This winding conduit is responsible for processing food, extracting essential nutrients, and disposing of waste in an ingenious manner:
Mouth: The journey commences here, where mechanical and chemical digestion starts as we chew and mix food with saliva.
Esophagus: Food then travels down the esophagus, which acts like a road leading to the stomach.
Stomach: Upon reaching the stomach, food undergoes thorough mixing and breakdown in an acidic environment, resulting in a gooey substance known as chyme.
Small Intestine: Chyme moves to the small intestine, the superstar of nutrient absorption, lined with tiny finger-like projections called villi that facilitate the transfer of nutrients into our bloodstream.
Large Intestine: Leftover waste enters the large intestine, where water is reabsorbed, and waste is compacted into feces, ready for elimination.
Anus: Finally, waste is expelled through the anus, completing the cycle of ingestion, digestion, and excretion.
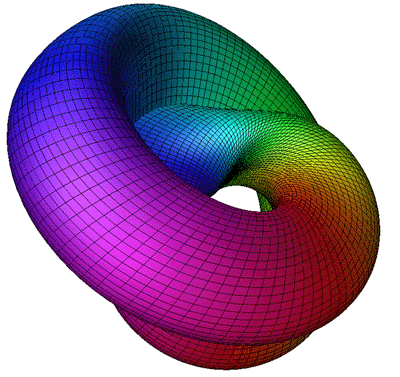
Like the hole in a donut, our mouth and anus serve as entry and exit points that allow our bodies to engage with the external environment. Within us lies a continuous tube, symbolizing the donut shape and emphasizing our unique internal structure.
Tubular Organ Connections: Our Anatomical Loop: Our anatomy features numerous interconnected systems. The alimentary canal serves as a hollow and continuous structure that reflects the topology of a donut. In a metaphorical sense, we become living donuts, with our internal structures mirroring the cyclical shape.
But Wait, There’s More! Enter the Six-Holed Donut
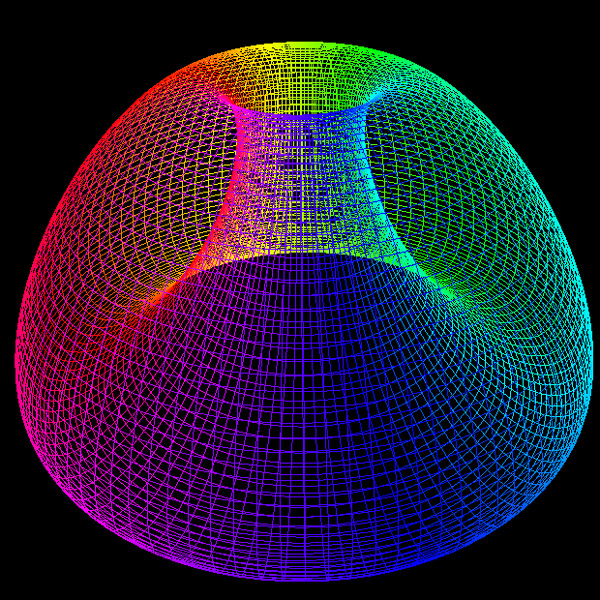
Upon zooming in to a microscopic scale of just 60 microns, the perception of the human body as a simple donut evolves into an even more intriguing concept: the human body is actually a six-holed donut! This unique structure can be shaped and extended into complex forms
Let’s designate one of these holes to represent the gastrointestinal (GI) tract, envisioning the mouth as the entry point that allows food to travel through our distinctive internal architecture. Next, we can roll half of the remaining orifices into this configuration. What emerges? A form reminiscent of the complex architecture of a human with seven openings converging at eight external orifices, all leading to a shared space: the nasal cavity!
If we consolidate all of the “matter” toward these tunnels, we notice something fascinating: our seven-hole torus is topologically equivalent to four pairs of pants sewn together at their waists. Yes, you heard it correctly! Rather than a straightforward donut, our bodies can be envisioned as an intricate bodysuit for a spider a whimsical yet insightful representation!
Now, to complete this remarkable shape, we can use two of the openings as nostrils, four more as tear ducts, and designate the final one as the mouth. By inflating this material into the form of a head and expanding the body shape to include an opening at the rear, we create an enthralling model that illustrates the complexity of human anatomy.
For the Nerds: A Technical Definition of a Donut
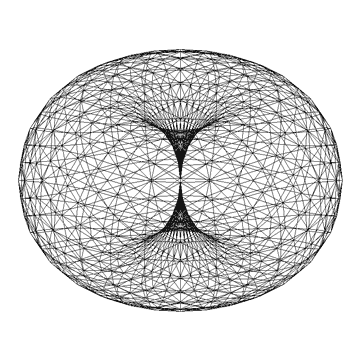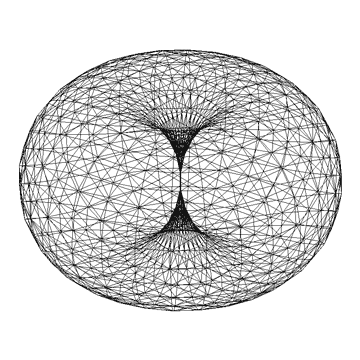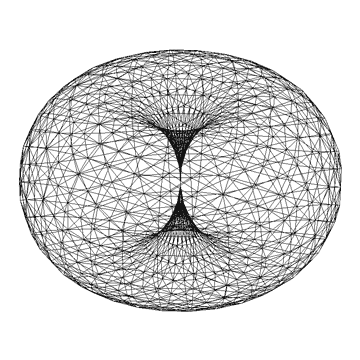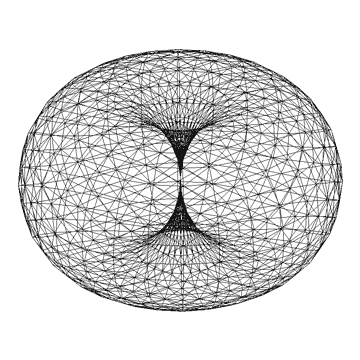
In mathematical terms, a donut is commonly referred to as a torus. The torus can be visualized as a circle rotating about an axis that lies in the same plane as the circle but does not intersect it.
Torus Parameterization: The mathematical equations defining a torus in three-dimensional space can be expressed in parametric form. Let us define two radii:
( R ): the distance from the center of the tube to the center of the torus (the major radius).
( r ): the radius of the tube itself (the minor radius).
The parametric equations for a torus, centered at the origin, can be given by:
[ x(\theta, \phi) = (R + r \cos \phi) \cos \theta ]
[ y(\theta, \phi) = (R + r \cos \phi) \sin \theta ]
[ z(\theta, \phi) = r \sin \phi ]
where ( \theta ) and ( \phi ) are variables that take values in the range [0, 2π]. This mathematical representation enhances our understanding of the toroidal shape's geometry and the underlying structures that can be compared to the human body.
Shapes That Can Be Considered Donuts
While traditional donuts are often round, various other shapes and planar figures can also be classified as donuts, so long as they maintain the essential characteristic of having a central void. Here are some examples:
Square Donuts: A square-shaped cross-section that spins around its center can create a toroidal shape, maintaining the essence of a donut while adopting a unique form.
Triangular Donuts: Similar to square donuts, a circular structure featuring triangular sections can form a toroidal figure when rotated around its centroid.
Irregular Torus: You can create a toroidal shape that varies in thickness or curvature, yet still features a continuous surface surrounding a central hollow space.
Where the Hole Begins and the Outer Shape Starts
In a toroidal shape, the distinction between the hole and outer structure is defined as follows:
Defining the Hole: The hole begins at the inner radius, where the circular path (or edge) of the inner tube forms the boundary of the hollow portion. Mathematically, this is characterized by the minor radius ( r ). The area encompassed by the inner circle contributes to the "hole" of the donut.
Defining the Outer Shape: The outer shape is defined by the outer radius, which represents the maximum extent of the toroidal surface, typically given by ( R + r ). This measurement includes the entire surface of the donut, excluding the hollow area.
When envisioning a standard donut, consider:
Inner Edge: The point where the donut’s material begins to curve inward toward the hole defines where the “hole” starts.
Outer Edge: The maximum width of the donut, extending away from the hole, marks the transition into its distinct outer shape.
Thus, a donut is defined as a toroidal shape characterized by its pivotal central hole and the continuous surface that encircles it. While most commonly round, alternative shapes can also exhibit donut-like properties while preserving a hollow core. The mathematical representation and geometric properties of the torus enrich our understanding of the definitions and characteristics of a donut and how we delineate its boundaries.
Through this exploration of the human "donut," we have unveiled compelling insights about our anatomy and the interconnectedness of life. Whether in humorous analogies or through serious scientific understanding, the relationship between our bodies and the natural world surrounding us continues to captivate our imaginations and drive our investigations into the mysteries of existence. So, the next time you think about your body, remember: it’s not just a donut; it’s a sophisticated, interconnected system that mirrors the complexity of life itself!